Inhalt

Netzwerkanalyse mit neo4j

Netzwerkanalyse mit neo4j

Technische Vorbemerkungen

(Dieses Kapitel wird gerade überarbeitet, da die Graph Algorithms Library durch die Graph Data Science Library abgelöst wurde. Die Befehle müssen hierfür noch angepasst werden.)

Um die Graphalgorithem in neo4j nutzen zu können, müssen sie installiert werden. Dies geschieht analog zur APOC-Library, wie im Anschnitt zur APOC-Installation erklärt.

Grundlagen zur Netzwerkanalyse

Vorbemerkungen

Bei der Netzwerkanalyse handelt es sich um einen relationalen Forschungsansatz, bei dem Methoden aus der Graphen- und Netzwerktheorie sowie der Statistik zur Anwendung kommen.¹ Aus den bisherigen Abschnitten sind Beziehungen (Kanten) von Entitäten (Knoten) in einem Netzwerk (Graph) bereits bekannt. Weitere wichtige Begriffe sind die Dyade als kleinste mögliche Analyseeinheit eines Netzwerkes. Sie umfasst alle möglichen Beziehungen zwischen zwei Knoten. Eine Triade bezieht alle möglichen Beziehungen zwischen drei Knoten mit ein. Bei einer Clique sind mindestens drei Knoten vollständig miteinander verbunden. Als Geodätischer Abstand (in neo4j shortest path) wird die kürzeste Verbindung zwischen zwei Knoten bezeichnet.

Überblick zu den Netzwerkmaßen

Grundlegende Maße in der Netzwerkanalyse sind

Dichte als Quotient zwischen tatsächlichen Anzahl der Kanten und der maximal möglichen Anzahl der Kanten.
Entfernungsmaße, z.B. geodätische Abstände, Durchmesser des Netzwerks etc.
Reziprozität als Quotient zwischen der Anzahl bidirektionaler und einseitiger Beziehungen.
Clustering beispielsweise als Anzahl und Art von Triaden.

Eine wichtige Rolle spielen auch die Zentralitätsmaße (Beispiele):

Bei der Degree Centrality werden pro Knoten die Anzahl der Verbindungen zu anderen Knoten betrachtet.
Bei der Betweenness Centrality wird die Anzahl der über einen Knoten laufenden möglichen Verbindungen zwischen zwei anderen Knoten erhoben.
Die Closeness Centrality erhebt die Nähe zu allen anderen Knoten.
Die Eigenvector Centrality misst die Verbindung zu “einflussreichen” Knoten.

Beispiel: Zentralitätsmaße

Die folgende Abbildung zeigt einen kleinen Beispielgraphen, an dem einige Zentralitätsmaße erklärt werden sollen.²

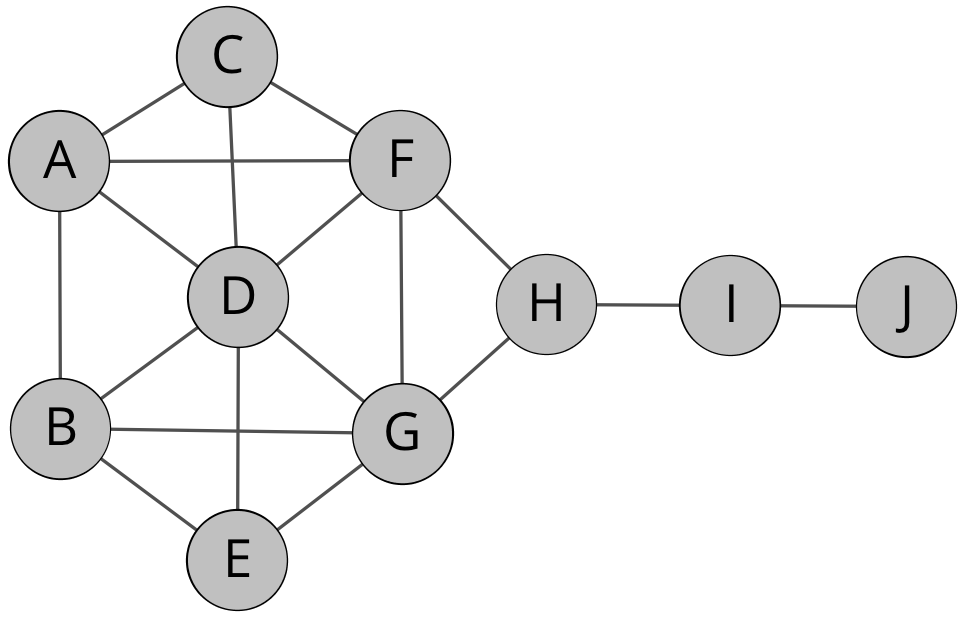
Beispielgraph für Zentralitätsmaße aus D. Krackhardt, Assessing the Political Landscape: Structure, Cognition, and Power in Organizations. Administrative Science Quarterly 35, 2, 1990, S. 351, http://dx.doi.org/10.2307/2393394.

Beispielgraph für Zentralitätsmaße aus D. Krackhardt, Assessing the Political Landscape: Structure, Cognition, and Power in Organizations. Administrative Science Quarterly 35, 2, 1990, S. 351.

Bei der Berechnung der Dichte wird der Quotient zwischen der tatsächlichen Anzahl der Kanten und der maximal möglichen Anzahl der Kanten berechnet. Die Formel hierfür lautet

Dichte des Netzwerks = 2m/(n*(n-1))

wobei m die Anzahl der vorhandenen Kanten ist und n die Anzahl der Knoten. Für unser Beispiel ergibt sich damit:

218/(10(10-1)) = 0,4

womit die Dichte des Netzwerks 0,4 beträgt.

Die höchste Degreeness Centrality hat mit 6 Kanten der Knoten D, was mehr als bei allen anderen ist. Den ersten Platz bei der Betweenness Centrality hat der Knoten H.
Die höchste Closeness besteht zwischen den Knoten F und G.
Der größte Eigenvector besteht zwischen den Knoten D, F und G.
Die Knoten F und G sind strukturell äquivalent.

Mit diesen Vorbemerkungen als Hintergrund werden in den folgenden Abschnitten Netzwerkanalyse-Algorithmen auf eine aufbereitete Graphdatenbank der Regesten Kaiser Heinrichs IV. angewendet.

Die Register der Regesta Imperii

Grundlage der hier verwendeten Netzwerkdaten sind die Nennungen von Personeneinträgen im Register der Regesten. Da die hier vorgestellten Netzwerkanalyse-Algorithmen nur mit unimodalen Netzwerken arbeiten können, also Netzwerken, die nur Knoten eines Typs enthalten, müssen die Regestendaten entsprechend erweitert werden. Dabei wird davon ausgegangen, dass zwei Personen, die gemeinsam in einem Regest genannt sind, etwas miteinander zu tun haben. Diese Verbindung wird durch eine APPEARS_WITH-Kante dargestellt, da die gemeinsame Rolle im Regest nicht näher qualifiziert werden kann.

Für die Netzwerkanalyse erstellen Sie mit Neo4j-Desktop eine Graphdatenbank der Version 4.1 oder höher, bei der Sie die Plugins APOC und Graph Data Science Library installieren. Zur Graph Data Science Library gibt es auch eine umfangreiche Dokumentation.

Für diesen Abschnitt werden als Datenbeispiel die Regesten Heinrichs IV. in einer Graphdatenbank verwendet. Die Erstellung der Graphdatenbank wird im Kapitel Regestenmodellierung im Graphen beschrieben. Auf dieser Datengrundlage werden dann noch zusätzliche Kantentypen erstellt. Mit dem folgenden Cypher-Query werden zwischen Personeneinträgen des Registers, die gemeinsam in einem Regest genannt sind, APPEARS_WITH-Kanten erstellt.

MATCH (n1:IndexPerson)-[r1:PERSON_IN]->
(:Regesta)<-[r2:PERSON_IN]-(n2:IndexPerson)
WHERE id(n1) <> id(n2)
WITH n1, count(r1) AS c, n2
CREATE (n1)-[k:APPEARS_WITH]->(n2)
SET k.count = c;

Zentralitätsalgorithmen in der historischen Netzwerkanalyse

Im folgenden Abschnitt werden verschiedene Zentralitätsalgorithmen zur Analyse der Personennetzwerke der Regesten Kaiser Heinrichs IV. verwendet. Im Zentrum steht hier zunächst die technische Anwendung. Die inhaltliche Analyse wird Gegenstand eines geplanten nächsten Kapitels sein. Als Vorlage für diesen Abschnitt diente u.a. das Buch Graph Algorithms von Mark Needham und Amy E. Hodler (O’Reilly Media 2019) und kann kostenlos auf dieser Seite bezogen werden: https://neo4j.com/graph-algorithms-book/. Es bietet einen sehr guten Überblick zur Nutzung von Netzwerkalgorithemn in neo4j.

PageRank

Der PagePageRank-Algorithmus bewertet und gewichtet eine Menge verknüpfter Knoten anhand ihrer Struktur.³ Auf Grundlage der Verlinkungsstruktur wird dabei jedem Knoten ein Gewicht, der sog. PageRank zugeordnet.

CALL algo.pageRank.stream("IndexPerson", "APPEARS_WITH",
{iterations:20})
YIELD nodeId, score
MATCH (node) WHERE id(node) = nodeId
RETURN node.name1 AS Person,
apoc.math.round(score,3)
ORDER BY score DESC;

Degree Centrality

MATCH (u:IndexPerson)
RETURN u.name1 AS name,
size((u)-[:APPEARS_WITH]->()) AS follows,
size((u)<-[:APPEARS_WITH]-()) AS followers
ORDER by followers DESC;

Betweenness Centrality

// betweenness centrality
CALL algo.betweenness.stream("IndexPerson",
"APPEARS_WITH", {direction: "OUTGOING", iterations: 10}) YIELD nodeId, centrality
MATCH (p:IndexPerson) WHERE id(p) = nodeId
RETURN p.name1 AS Name, centrality
ORDER by centrality DESC;

Closeness Centrality

// betweenness centrality
CALL algo.closeness.stream("IndexPerson", "APPEARS_WITH")
YIELD nodeId, centrality
MATCH (n:IndexPerson) WHERE id(n) = nodeId
RETURN n.name1 AS node, apoc.math.round(centrality,2)
ORDER BY centrality DESC
LIMIT 30;

Community Detection Algorithmen

Strongly Connected Components

CALL algo.scc.stream("IndexPerson","APPEARS_WITH")
YIELD nodeId, partition
MATCH (u:IndexPerson) WHERE id(u) = nodeId
RETURN u.name1 AS name, partition
ORDER BY partition DESC;

Weakly Connected Components

CALL algo.unionFind.stream("IndexPerson","APPEARS_WITH")
YIELD nodeId, setId
MATCH (u:IndexPerson) WHERE id(u) = nodeId
RETURN u.name1 AS name, setId;

Label Propagation

CALL algo.labelPropagation.stream("IndexPerson",
"APPEARS_WITH", {direction: "OUTGOING", iterations: 10})
YIELD nodeId, label
MATCH (p:IndexPerson) WHERE id(p) = nodeId
RETURN p.name1 AS Name, label ORDER BY label DESC;

Louvain Modularity

CALL algo.louvain.stream("IndexPerson",
"APPEARS_WITH", {})
YIELD nodeId, community
MATCH (user:IndexPerson) WHERE id(user) = nodeId
RETURN user.name1 AS user, community
ORDER BY community;

Triangle count and Clustering Coefficient

CALL algo.triangle.stream("IndexPerson","APPEARS_WITH")
YIELD nodeA,nodeB,nodeC
MATCH (a:IndexPerson) WHERE id(a) = nodeA
MATCH (b:IndexPerson) WHERE id(b) = nodeB
MATCH (c:IndexPerson) WHERE id(c) = nodeC
RETURN a.name1 AS nodeA, b.name1 AS nodeB, c.name1 AS node;

direkt aus dem Beispiel übernommen

CALL algo.triangleCount.stream('IndexPerson', 'APPEARS_WITH')
YIELD nodeId, triangles, coefficient
MATCH (p:IndexPerson) WHERE id(p) = nodeId
RETURN p.name1 AS name, triangles, coefficient
ORDER BY coefficient DESC;

nach der Anzahl der Dreiecksbeziehungen sortiert

CALL algo.triangleCount.stream('IndexPerson', 'APPEARS_WITH')
YIELD nodeId, triangles, coefficient
MATCH (p:IndexPerson) WHERE id(p) = nodeId
RETURN p.name1 AS name, triangles, coefficient
ORDER BY triangles DESC;

CALL algo.labelPropagation.stream("IndexPerson",
"APPEARS_WITH", {direction: "OUTGOING", iterations: 10})
YIELD nodeId, label
MATCH (p:IndexPerson) WHERE id(p) = nodeId
RETURN p.name1 AS Name, label ORDER BY label DESC;

CALL algo.triangle.stream("IndexPerson","APPEARS_WITH")
YIELD nodeA,nodeB,nodeC
MATCH (a:IndexPerson) WHERE id(a) = nodeA
MATCH (b:IndexPerson) WHERE id(b) = nodeB
MATCH (c:IndexPerson) WHERE id(c) = nodeC
RETURN a.shortName AS nodeA, b.shortName AS nodeB, c.shortName AS node;

Zusammenfassung

In diesem Kapitel wurde die im Kapitel zur Graphmodellierung eingerichtete Graphdatenbank mit den Regesten Kaiser Heinrichs IV. für die Anwendung von Netzwerkanalyse-Algorithmen vorbereitet. Im zweiten Abschnitt wurden dann Cypher-Queries für verschiedene Netzwerkalgorithmen aufgelistet. In einem weitern geplanten Kapitel werden die Ergebnisse dieser Algorithmen qualitativ ausgewertet.

Die Informationen und Abbildungen in diesem Abschnitt stammen aus dem Kurs Historisch-archäologische Netzwerkanalyse von Aline Deicke und Marjam Trautmann, der im Rahmen der International Summer School in Mainz stattfand (abgerufen am 07.02.2019). ↩
Vgl. zu diesm Abschnitt D. Krackhardt, Assessing the Political Landscape: Structure, Cognition, and Power in Organizations. Administrative Science Quarterly 35, 2, 1990, S. 342-369 (abgerufen am 07.02.2019). ↩
Zu PageRank vgl. https://de.wikipedia.org/wiki/PageRank. ↩